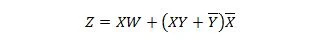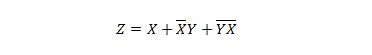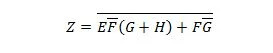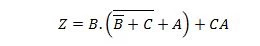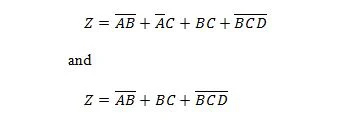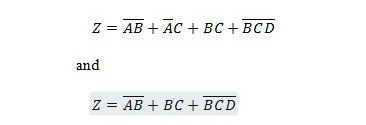Поглавље 2: Булова алгебра и њене повезане рачунарске компоненте
2.1 Основни логички оператори
Претпоставимо да сам ја (аутор) висок, а ти (читалац) висок. Ако вас неко пита да ли смо обоје високи, рекли бисте „Да“ (тачно). Ако он пита да ли смо обоје ниски, рекли бисте „Не“ (нетачно). Ако сте ви ниски, а ја висок, а он вас пита да ли сте ви или ја високи, ваш одговор би био „Да“ (тачно). Ако он пита да ли смо и ти и ја високи, не бисте имали одговор. Можете наставити да кажете да последње питање не треба да се поставља или да питање нема одговор. Па, желим да ви (читалац) знате да данас, под одређеним околностима, треба поставити питање.
У биологији, особа је или висока или ниска. Услови „окружења” чине особу средње висине. Један научник, Џорџ Бул, дефинисао је скуп одговора или правила за ову врсту питања. Ова правила ћемо научити у овом одељку онлајн курса за каријеру (поглавље). Ова правила се данас користе у рачунарству, програмирању, електроници и телекомуникацијама. У ствари, без ових правила не бисте имали рачунар, као што је то данас уобичајено; не бисте имали и програмирање, као што је то данас уобичајено.
Тачно или Нетачно
Једноставна изјава на људском језику је или истинита или лажна сама по себи. Ако кажем, „висок сам“, то је или тачно или нетачно. Ако кажем, „висок си“, то је или тачно или нетачно. Ако сам ја висок, а ти ниски, и поставља се питање да ли смо и ти и ја високи, у Буловој логици мора се дати одговор тачан или нетачан. Које од ово двоје треба дати? Бул није баш одговорио на ово питање. Он је једноставно смислио скуп правила која треба да се придржавамо. Добра вест је да, када пратите ова правила у њиховом правом контексту, немате никакву двосмисленост. Захваљујући овим правилима, данас имамо рачунаре и програмирање. Правила су вам сада дата. Правила се заиста не могу објаснити; само их прихватите. Правила су под три наслова: И, ИЛИ и НЕ.
И
Може се поставити питање да ли сте и ви и ја високи. Моја висина и ваша висина се затим комбинују помоћу АНД скупа правила. Ово су И правила која треба следити:
нетачно И лажно = лажно
нетачно И тачно = нетачно
тачно И нетачно = нетачно
тачно И тачно = тачно
Сада, нека високо буде истинито, а кратко лажно. То значи да ако сам ја низак И ти си низак, ти и ја смо кратки. Ако сам ја низак А ти си висок, ти и ја смо ниски; то је Булов одговор који морате да прихватите. Ако сам ја висок А ти си низак, ниски смо и ти и ја. Ако сам ја висок И ти си висок, ти и ја смо високи. Све су то И Булова правила која ви (читалац) једноставно морате да прихватите.
ИЛИ
Може се поставити питање да ли сте ви ИЛИ ја висок. Моја висина и ваша висина се затим комбинују помоћу ИЛИ скупа правила. Ово су ИЛИ правила која треба следити:
фалсе ОР фалсе = лажно
нетачно ИЛИ тачно = тачно
тачно ИЛИ нетачно = тачно
тачно ИЛИ тачно = тачно
Опет, нека високо буде истинито, а кратко нетачно. То значи да ако сам ја низак ИЛИ ти си низак, ти ИЛИ ја сам низак. Ако сам ја низак ИЛИ си ти висок, ти или ја смо високи. Ако сам ја висок ИЛИ си ти низак, ти ИЛИ ја сам висок. Ако сам ја висок ИЛИ си ти висок, ти или ја смо високи. Све су ово Булова правила која морате да прихватите.
НЕ
Сада, у Буловој логици, постоје само два стања (могући одговори). То јест, ако НИСИ висок, низак си. Ако НИСИ низак, висок си; ништа друго. Ово НИСУ правила која треба следити:
НИЈЕ нетачно = тачно
НИЈЕ тачно = нетачно
Претпоставимо да имате врпцу (или опругу) коју можете продужити (повући). Док је стринг у свом природном стању, ако кажем, „НЕ кратка“, продужили бисте га; то је тумачење. Док је стринг продужен, ако кажем, „НЕ дугачак“, дозволили бисте му да се скупи; то је тумачење.
Морате запамтити сва дата правила у њиховим различитим категоријама.
Више од два операнда
У рачунарском језику, И, ИЛИ и НОТ се називају оператори. За НОТ оператор, потребан вам је само један операнд (вредност за оператор) да бисте имали одговор. За операторе АНД или ОР, можете имати више од два операнда. Претходни случајеви показују два операнда за АНД и ОР. Можете имати три операнда за И на следећи начин:
лажно И лажно И лажно = лажно
нетачно И нетачно И тачно = нетачно
Ово су две линије; сваки има два АНД оператора. У ствари има девет редова када су операнди три. Са оператором АНД, само последњи ред (девети ред) је једнак истинитом; сви претходни редови су нетачни. Имајте на уму да је са два операнда за И само последњи ред још увек истинит; сва претходна три реда су нетачна. Када су операнди четири, има 16 линија и само последња линија је тачна за оператор АНД.
Образац за И и образац за ОР се разликују. Са три операнда за два ОР оператора, постоји и девет линија и само је први ред, овога пута, нетачан. Од другог до деветог реда је тачно. Имајте на уму да је са два операнда за ОР само први ред још увек истинит; све преостале три линије су нетачне. Када су операнди четири за ОР, постоји и 16 линија.
Оператор НОТ ради само са једним операндом. Нетачно је тачно, а НЕтачно је лажно.
2.2 Табела истинитости два операнда и њихове електронске компоненте
У математици постоји тема која се зове алгебра. Мали део тога је виђен у претходном поглављу. Постоји врста алгебре која се зове Булова алгебра. У Буловој алгебри, тачно се идентификује основном две цифре која је 1, а нетачно се идентификује основном две цифре која је 0.
Компоненте унутрашње рачунарске јединице су електронске компоненте. Системска јединица рачунарског система има дигиталне електронске компоненте. Операцију И врши мала електронска компонента која се зове И капија. Операцију ИЛИ врши мала електронска компонента која се зове ОР капија. Операцију НОТ врши мала електронска компонента која се зове НОТ капија. Превише ових капија може бити у чипу са интегрисаним колом (ИЦ).
И Трпеза истине и њена капија
Следећа табела даје табелу истине И и њен симбол АНД капије (мало коло):
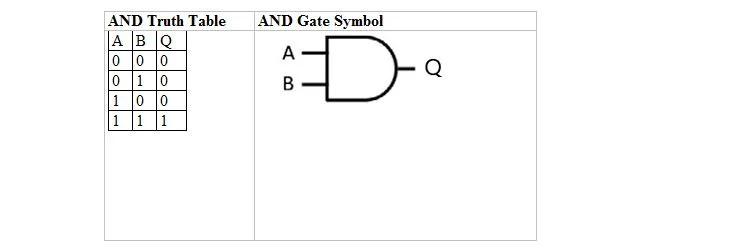
И за табелу истине И и за њену капију, А као и Б су две улазне варијабле. К је излазна променљива. А је или 1 или 0. Б је или 1 или 0. К је или 1 или 0. И табела истинитости са 1 и 0 је иста као претходни распоред истинитих/нетачних И (табела). И једначина је:
А. Б = К
где тачка (.) значи И (Боолеан). Тачка се може изоставити да има АБ = К што значи исту ствар (И).
Напомена: Битови за А и Б у четири реда, као парови, су прва четири броја у бази два која почињу од 0 (или 00), тј. 00, 01, 10, 11.
Следећа табела даје табелу истине ИЛИ и њен симбол капије ИЛИ (мало коло):
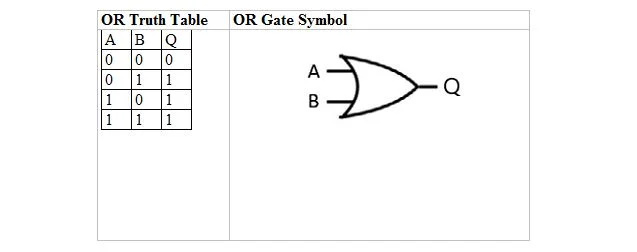
И за табелу истине ИЛИ и за њену капију, А као и Б су две улазне варијабле. К је излазна променљива. Табела истине ИЛИ са 1 и 0 је иста као претходни изглед истинитог/нетачног ИЛИ (табела).
ОР једначина је:
А + Б = К
Где + овде значи логички ОР а не сабирање. Једначина се чита као „А или Б једнако К“.
Следећа табела даје табелу истине НЕ и њен симбол НЕ капије (мало коло):
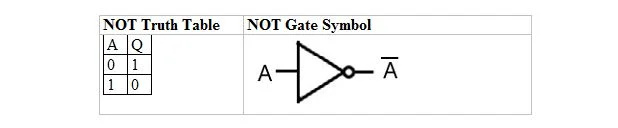
Табела истине НЕ или НОТ капија има само један улаз и један излаз. Када је улаз 0, излаз је 1. Када је улаз 1, излаз је 0. НОТ капија врши неку врсту инверзије. Излазна променљива је иста као и улазна променљива, али са траком (прекочена). Табела истине НЕ са 1 и 0 је иста као претходни распоред истинито/нетачно ИЛИ (табела).
Једначина НЕ је:
А = К
Где К = А и пречка изнад А овде значи комплемент. Комплемент од 0 је 1, а комплемент од 1 је 0. НОТ капија је позната и као ИНВЕРТИРАЈУЋА капија.
Ово су основне (или коренске) табеле истине и њихове капије (мала кола) у дигиталној електроници (са Буловом алгебром). Остале три табеле истинитости које су дате на следећој илустрацији и њихове капије су ради практичности и засноване су на претходне три табеле истинитости.
Постоји табела истине и капија који су изведени из табеле и капије истине И. Они се називају НАНД (за НЕ И) табела истине и одговарајућа НАНД капија. НАНД табела истине и њена НАНД капија су:
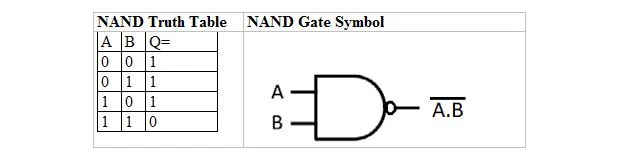
Да бисте добили НАНД табелу истинитости, идите на излаз АНД табеле истинитости и замените сваку цифру њеним комплементом. Комплемент од 0 је 1, а комплемент од 1 је 0. НАНД капија је као капија И, али има мали круг испред излазне линије. НАНД једначина је:
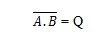
Где значи допуну резултата „А“ И „Б“. Пречка (преко линије) је у капији представљена малим кругом. Имајте на уму да се тачка између А и Б може изоставити.
Постоји још једна табела истине и капија који су изведени из табеле истине ИЛИ и капије. Они се називају НОР (за НЕ ИЛИ) табела истине и одговарајућа НОР капија. Табела истине НОР и њена НОР капија су:
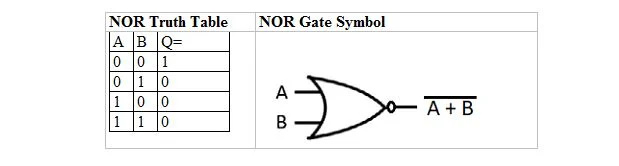
Да бисте добили табелу истинитости НОР, идите на излаз табеле истинитости ИЛИ и замените сваку цифру њеним комплементом. Комплемент од 0 је 1, а комплемент од 1 је 0. НОР капија је као капија ИЛИ, али има мали круг испред излазне линије. НОР једначина је:
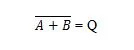
Где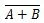 
означава допуну резултата „А” ИЛИ „Б”. Пречка (оверлине) је представљена на капији малим кругом.
Искључиво ОР (КСОР)
Табела истине за капију ОР је:
У нормалном енглеском, није јасно да ли последњи ред од 1 ИЛИ 1 треба да даје 1 или 0. Дакле, у Буловој алгебри, постоје две врсте табела истине ИЛИ и две одговарајуће капије. Са нормалним ОР, последњи ред од 1 ИЛИ 1 даје 1. Други тип ОР је ексклузивно ИЛИ (КСОР) где су прва три реда иста као прва три реда нормалног ОР (укључујући излаз). Међутим, за четврти и последњи ред, 1 ИЛИ 1 даје 0.
Следећа табела даје КСОР табелу истинитости и њен симбол КСОР капије (мало коло):
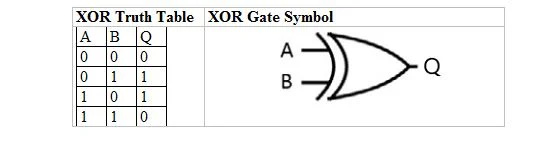
И за КСОР табелу истинитости и за њену капију, „А“ као и „Б“ су две улазне варијабле. „К“ је излазна варијабла.
КСОР једначина је:
А ⊕ Б = К
Где ⊕ овде значи Булов КСОР.
Нормално ИЛИ значи једно или обоје. Искључиво ИЛИ значи строго било а не обоје.
2.3 Булови постулати
Постулати су претпоставке на основу којих се изводе одређени закључци. Постоји десет Булових постулата који су укорењени из И, ИЛИ и НЕ једначина (табела истинитости). Ове једначине се називају и функције. Основне функције су копиране на следећи начин:
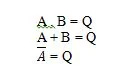
Ово су основне функције (једначине) у Буловој алгебри. Следеће три (функције) једначине нису фундаменталне функције:
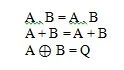
Иако је последња функција овде необична, она се не сматра основном функцијом.
Булови постулати су следећи:
Од функције И
1) 0 . 0 = 0
двадесет . 1 = 0
3) 1. 0 = 0
4) 1. 1 = 1
Из функције ОР
5) 0 + 0 = 0
6) 0 + 1 = 1
7) 1 + 0 = 1
8) 1 + 1 = 1
Из НОТ функције
9) 0 = 1
10) 1 = 0
Белешка: Ови постулати су само линије у табелама истине И, ИЛИ и НЕ које су изражене на независан начин. Читалац треба да запамти дате постулате.
2.4 Булова својства
Својство је као карактеристика нечега. Булова својства су једначине које су изведене из Булових постулата. У овом одељку, својства су једноставно дата без њихових извођења и затим се користе. Постоји двадесет пет некретнина које су груписане под десет наслова на следећи начин:
Особине функције АНД
Својство 1:
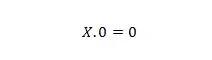
Где Кс може бити 1 или 0. То значи да без обзира шта је Кс, резултат је увек 0.
Напомена: Променљива не сме нужно бити А или Б или Ц или Д. Променљива може бити В или Кс или И или З или било које друго слово.
Својство 2:
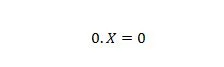
Где Кс може бити 1 или 0. Имајте на уму да је разлика између својства 1 и својства 2 у томе што се на левој страни знака једнакости обе једначине, позиције Кс и 0 замењују.
Својство 3:
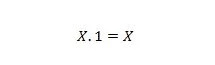
Ако је Кс 0, онда је 0. 1 = 0. Ако је Кс 1, онда је 1. 1 = 1.
Својство 4:
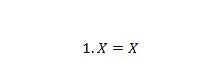
Ако је Кс 0, онда је 1. 0 = 0. Ако је Кс 1, онда је 1. 1 = 1. Имајте на уму да је разлика између својства 3 и својства 4 у томе што су на левој страни обе једначине позиције Кс и 1 се замењују.
Особине функције ОР
Својство 5:
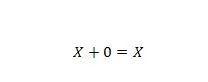
Где Кс може бити 1 или 0. То значи да ако је Кс 0, резултат је 0. Ако је Кс 1, резултат је 1.
Својство 6:
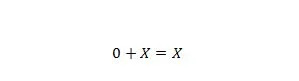
Где Кс може бити 1 или 0. Имајте на уму да је разлика између својства 5 и својства 6 у томе што су на левој страни обе једначине позиције Кс и 0 замењене.
Својство 7:
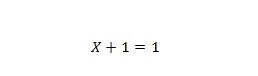
Ако је Кс 0, онда је 0 + 1 = 1. Ако је Кс 1, онда је 1 + 1 = 1.
Својство 8:
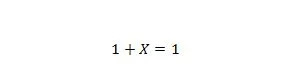
Ако је Кс 0, онда је 1 + 0 = 1. Ако је Кс 1, онда је 1 + 1 = 1. Имајте на уму да је разлика између својства 7 и својства 8 у томе што су на левој страни обе једначине позиције Кс и 1 се замењују.
Својства у вези са комбинацијом променљиве са собом или њеним комплементом
Својство 9: 
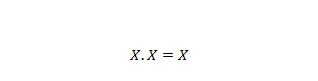
То јест: ако је Кс 0, онда је 0. 0 = 0. Ако је Кс 1, онда је 1. 1 = 1.
Својство 10:
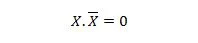
То јест: ако је Кс 0, онда је 0. 1 = 0. Ако је Кс 1, онда је 1. 0 = 0.
За узастопне варијабле, ово својство постаје:
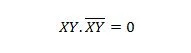
Својство 11:
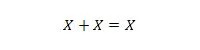
То јест: ако је Кс 0, онда је 0 + 0 = 0. Ако је Кс 1, онда је 1 + 1 = 1 (од нормалног ИЛИ).
Својство 12:
То јест: ако је Кс 0, онда је 0 + 1 = 1. Ако је Кс = 1, онда је 1 + 0 = 1.
То јест: ако је Кс 0, онда је 0 + 1 = 1. Ако је Кс = 1, онда је 1 + 0 = 1.
Двострука допуна
Својство 13:
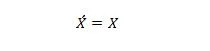
Када је Кс на левој страни 0, Кс на десној страни постаје 0. Када је Кс на десној страни 1, Кс на левој страни постаје 1. Другим речима, двоструки комплементи враћају првобитну вредност.
Цоммутативе Лав
Својство 14:
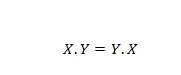
То значи да замена првог и другог операнда за АНД оператор, на левој страни знака једнакости, није битна; одговор је и даље исти након што је дошло до размене на левој страни. Ова једначина се може написати са изостављеним тачкама као: КСИ = ИКС.
Својство 15:
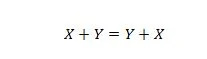
Објашњење овде је исто као у претходном И, али је за ОР оператор.
Дистрибутивно право
Својство 16:
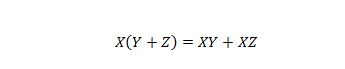
Овде постоје три променљиве: Кс, И и З. Свака променљива може бити 1 или 0. На левој страни симбола једнакости, заграде значе да се прво процени шта је у њима. Тада је И резултат са Кс. Десна страна каже да су Кс И И заједно, ИЛИ Кс И З заједно, исто што и лева страна. Имајте на уму да је оператор тачке за АНД-ове изостављен до краја; а спојене варијабле и даље значе И.
Својство 17:
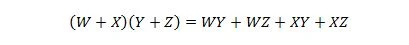
Ово својство је проширење својства 16 са додатом променљивом В.
Асоцијативно право
Својство 18:
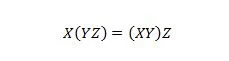
Заграде значе да се прво процени шта је у заградама. Дакле, за израз на левој страни, ако је И са З прво АНД, а Кс је АНД са резултатом, онда је коначни резултат на левој страни исти као и коначни резултат на десној страни -ханд-сиде где је Кс са И прво АНД пре АНД резултата са З. Имајте на уму да су тачке изостављене у једначини.
Својство 19:
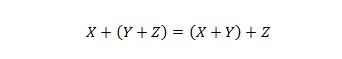
Ово својство је објашњено на сличан начин као својство 18, али се уместо АНД оператора користи ОР оператор. Оператор ОР + се никада не изоставља из Буловог израза ради једноставности. С друге стране, АНД оператор се може изоставити и две варијабле се могу спојити.
Апсорпција
Својство 20:
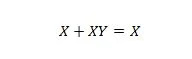
Са овом једначином, без обзира шта је И, десна страна ће увек бити Кс (апсорбована).
Својство 21:
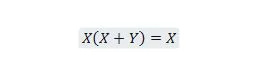
Такође, са овом једначином, без обзира шта је И, десна страна ће увек бити Кс (апсорбована). Ово својство 21 је исто као и својство 20 које је:
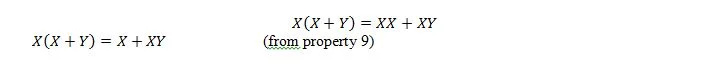
Овде користимо дистрибутивни закон и чињеницу да је Кс.Кс = Кс својства 9.
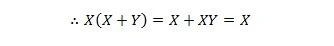
Ан Идентити
Својство 22:
То значи да за израз Кс + И, допуна Кс испред И не мења израз.
Својство 23:
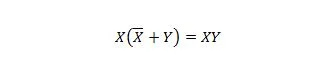
То значи да за КСИ израз, допуна Кс ОР са И у заградама, што се прво ради, не мења КСИ израз.
ДеМорганов закон
Својство 24:
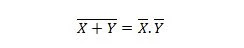
То значи да капија НОР (НЕ ИЛИ) има исти резултат као да се забрањују два улаза пре него што их АНД.
Својство 25:
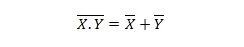
То значи да НАНД (НЕ И) капија има исти резултат као и НОТирање два улаза пре ИЛИ.
Достављене илустрације су 25 некретнина. Они се могу доказати заменом свих различитих могућих вредности 1 и 0, у сваком изразу на левој страни, да би се видело да ли се добија израз (или резултат) на десној страни. Докатуре су остављене као вежба за читаоца.
2.5 Поједностављење сложених израза
Следеће две функције су исте:
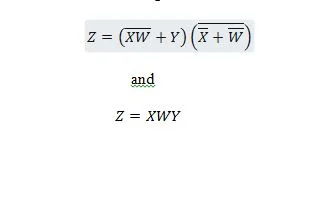
З је излаз, а Кс, В и И су улази. Првој је потребна НАНД капија, ИЛИ капија, И капија, две НЕ капије, ИЛИ капија и НОР капија. За другу су потребне само две И капије. Прва је једначина са сложеним изразом, на десној страни, која је поједностављена (сведена) на један израз десног израза за другу једначину.
Поједностављење или редукција доводи до мањег броја капија како би се имплементирала иста функција као и коло. Тако мање коло може бити део интегрисаног кола (ИЦ) или бити самостално коло на површини матичне плоче рачунара.
Када функција (једначина) стигне у процес пројектовања, мора се извршити поједностављење да би се смањио број капија и на крају добило јефтиније коло. Поједностављење захтева коришћење једног или више од претходних двадесет пет Булових својстава.
Пример 2.51:
Смањите једначину:
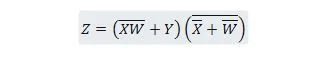
Белешка: Две заграде једна поред друге значе да су заграде означене И (тачка између њих опционо није уписана).
Решење:
За решења, оправдање (разлог) за сваки корак је дато десно од корака, у заградама. Читалац треба да прочита сваки корак и његову оправданост. Читалац такође треба да се позове на претходна својства док чита кораке редукције функције.
Пример 2.52:
Поједноставити:
2.6 Минимални збир производа
Следеће две функције су исте:
За оба десна израза обе једначине се каже да су у облику збира производа (СП). За експресни израз се каже да је у облику Збира производа ако нема заграде. Очигледно је да је за прву функцију (једначина) потребно више капија него за другу функцију.
Први десни израз се још увек може смањити да би се добила друга функција. Други израз са десне стране се не може даље поједностављивати и још увек може бити изражен као збир производа („сабирање“ појмова). Други израз са десне стране се заиста не може даље упрошћавати. Дакле, каже се да је у облику минималне суме производа (МСП).
Пример 2.61:
Доведите следећу функцију прво у образац за збир производа, а затим у образац за минималну суму производа.
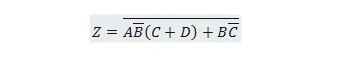
Решење:
Приликом решавања оваквих задатака, једно или више од претходних двадесет и пет својстава се мора користити као што је илустровано у овом решењу:
2.6 Минимални збир производа
Следеће две функције су исте:
За оба десна израза обе једначине се каже да су у облику збира производа (СП). За експресни израз се каже да је у облику Збира производа ако нема заграде. Очигледно је да је за прву функцију (једначина) потребно више капија него за другу функцију.
Први десни израз се још увек може смањити да би се добила друга функција. Други израз са десне стране се не може даље поједностављивати и још увек може бити изражен као збир производа („сабирање“ појмова). Други израз са десне стране се заиста не може даље упрошћавати. Дакле, каже се да је у облику минималне суме производа (МСП).
Пример 2.61:
Доведите следећу функцију прво у образац за збир производа, а затим у образац за минималну суму производа.
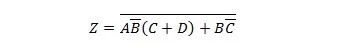
Решење:
Приликом решавања оваквих задатака, једно или више од претходних двадесет и пет својстава се мора користити као што је илустровано у овом решењу:
Овај последњи израз је у облику Збира производа (СП), али не и у облику Минималне Суме производа (МСП). На први део питања је одговорено. Решење за други део је следеће:
Ова последња поједностављена функција (једначина) је у МСП облику, и потребан јој је мањи број капија за имплементацију од одговарајућег СП облика. Запамтите: СП значи збир производа, док МСП значи минимални збир производа.
Пример 2.62:
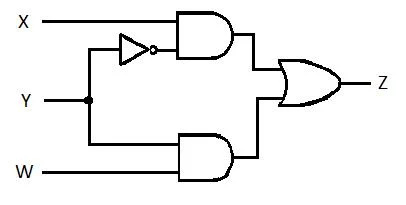
Следеће коло има Кс, И и В улазе, а З је излаз. Произвести функцију Збира производа (СП) (привидна функција минималне суме производа) за З. Затим произвести прави, смањени (минимизирани) збир производа (МСП). Затим имплементирајте МСП коло (нацртајте МСП гејтинг мрежу).
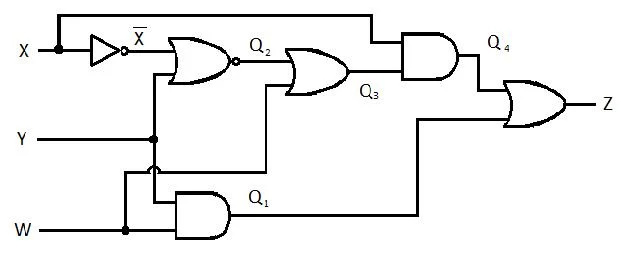
Слика 2.61 А творнички круг
Решење:
Пре него што започне процес поједностављења, израз за З се мора добити у терминима Кс, И и В. Погледајте овај пример илустрације са дијаграма:
Ово је израз З у терминима Кс, И и В. Након тога, може доћи до поједностављења на привидни МСП. Очигледни МСП је СП.
Ова последња једначина (функција) је у СП облику. Није тачно Минимални збир производа (још није МСП). Дакле, редукција (минимизација) мора да се настави.
Ова последња једначина (функција) је прави минимални збир производа (МСП). А минимални збир производа (истински минимизирај) гејтинг коло је:
Слика 2.62 МСП отворно коло
Коментар
Из анализе у овом одељку може се видети да није јасно да ли је збир производа минимални збир производа или не. СП није много користан. Управо је МСП веома користан. Постоји сигуран начин да се добије МСП; то је да се користи Карнаугх мапа. Карнаугх мапа је ван оквира овог онлајн курса за каријеру.
2.7 Проблеми
Читаоцу се саветује да реши све проблеме у једном поглављу пре него што пређе на следеће поглавље.
- Направите табеле истине И, ИЛИ и НЕ са њиховим одговарајућим капијама.
- Запишите десет Булових постулата у њиховим различитим категоријама, именујући категорије.
- Без објашњења, запишите двадесет и шест својстава Булове алгебре у њиховим различитим категоријама, именујући категорије.
- Смањите једначину користећи Булова својства и цитирајући коришћене категорије.
- Смањите једначину користећи Булова својства и цитирајући коришћене категорије.
- Користећи Булова својства и цитирајући коришћене категорије, смањите следећу једначину – прво на збир производа, а затим на минимални збир производа:
- Користећи Булова својства и цитирајући коришћене категорије, смањите следећу једначину – прво на збир производа, а затим на минимални збир производа:
